Una función puede considerarse como un caso particular de una relación o de correspondencia matemática. Cada relación o correspondencia de un elemento  con un (y sólo un)
con un (y sólo un)  se denota
se denota  , en lugar de
, en lugar de 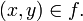
Formalmente, pedimos que se cumplan las siguientes dos condiciones:
|
Ejemplos
- La función definida por
 , tiene como dominio, codominio e imagen a todos los números reales
, tiene como dominio, codominio e imagen a todos los números reales 
- Para la función
 tal que
tal que  , en cambio, si bien su dominio y codominio son iguales a
, en cambio, si bien su dominio y codominio son iguales a  , sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
, sólo tendrá como imagen los valores comprendidos entre 0 y +∞.
- En la figura se puede apreciar una función
 , con
, con
- Note que a cada elemento de X le corresponde un único elemento de Y. Además, el elemento a de Y no tiene origen, y el elemento b tiene dos (el 1 y el 4). Finalmente,
- Esta función representada como relación, queda:

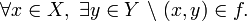



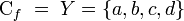

No hay comentarios:
Publicar un comentario